가능도(Likelihood)

이번 포스팅에서는 "가능도(Likelihood)" 에 대해서 정리해보려 한다.

가능도(Likelihood)의 정확한 개념과 더불어, "가능도"와 "확률"의 차이점에 대해 한 번 정리를 해보려 한다.

우선 확률(Probability)과 가능도(Likelihood)의 정의를 살펴보면 다음과 같다.

확률: 주어진 확률분포에서 해당 관측값이 나올 확률
가능도: 주어진 관측값이 특정 확률분포로부터 나왔을 확률 (= 연속확률밀도함수의 y 값)

음.. 이렇게 한 줄로 된 정의만 보면 무슨 말인지 통 이해가 안 될 것이다...
(위 정의만으로 이해가 된다면 그 분은 아마도 통계학 전공자일 것이다)


자, 그러면 "확률(Probability)"의 개념부터 천천히 설명해 보도록 하겠다.

"확률"이란 주어진 확률분포가 있을 때, 관측값 혹은 관측 구간이 분포 안에서 얼마의 확률로 존재하는 지를 나타내는 값이다. 여기서 중요한 점은 확률분포가 주어졌을 때의 관측값 X에 대한 확률을 구한다는 것이다. 이를 수식으로 표현해보면 아래와 같다.

수식으로 나타낸 확률의 정의

그렇다면 "가능도(Likelihood)"란 도대체 무엇일까?

"가능도"는 어떤 값이 관측되었을 때, 해당 관측값이 어떤 확률분포로부터 나왔는지에 대한 확률이다. 즉, "확률"의 개념과는 반대로 고정되는 요소가 확률분포가 아닌 관측값 X인 것이다.

수식으로 나태난 가능도의 정의

위 설명들을 직관적으로 이해하기 쉽게 그래프로로 그려보면 아래와 같다!

그림으로 살펴본 확률과 가능도의 정의

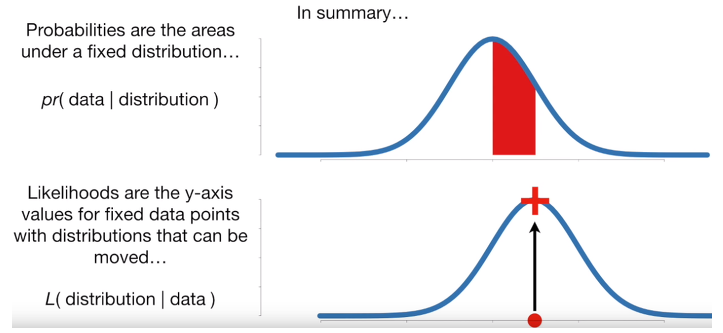
이제 "확률"과 "가능도"의 개념에 대해서 어느 정도 이해를 했을 것이라 생각한다.


마지막으로 "최대 가능도 추정(Maximum Likelihood Estimation)"이란 무엇인지 설명하고 이번 포스팅을 마무리 하도록 하겠다.

"최대 가능도 추정"이란 한 마디로 각 관측값 X에 대한 총 가능도(즉, 모든 가능도의 곱)가 최대가 되게 하는 확률분포를 찾는 것이라고 할 수 있겠다. 여기서 중요한 점은 최대 가능도 추정(Maximum Likelihood Estimation) 시, 먼저 임의의 확률분포를 가정해야 한다는 것이다.

이해를 돕기 위한 예시로 정규분포를 가정하고 최대 가능도 추정에 대하여 설명해 보도록 하겠다.

아래와 같이 여러 개의 관측값들이 존재할 경우, 이렇게 관측될 가능성이 가장 높은 확률분포를 찾는다고 해보자.

우리가 찾고자 하는 확률분포가 정확히 뭔지는 모르지만, 위에서 "정규분포"라고 가정을 했다. 그러므로 정규분포의 평균을 조금씩 증가시킬 때마다 가능도가 어떻게 변하는지 확인해보면 다음과 같다.

위 그림을 통해, 우리가 수집한 관측값들이 나올 수 있는 가장 가능성 높은(즉, 가장 가능도가 큰) 확률분포는 검은 점이 제일 높이 위치한(그림에서 노란색으로 표시된 부분) 정규분포로부터 온 것이라고 추정할 수 있다. 이러한 방식으로 확률분포를 추정하는 방법을 "최대 가능도 추정"이라고 한다.

이번 포스팅에서는 다소 어려운(?) 개념인 "가능도(Likelihood)"에 대해 정리해 보았다. 한 번에 잘 이해가 되지 않는다고 좌절하지 말고, 본 포스팅을 천천히 읽다 보면 개념을 잡을 수 있을 것이다!


<Reference>
https://jjangjjong.tistory.com/41

확률(probability)과 가능도(likelihood) 그리고 최대우도추정(likelihood maximization)