이번 포스팅은 Decision Tree에 대해서 진행하도록 하겠다.
자, 그럼 오늘도 시작해보겠다!!
▶ 결정 트리 학습과 시각화
- 사이킷런의 DecisionTreeClassifier(분류)와 DecisionTreeRegressor(회귀)를 사용한다.
- export_graphviz( ) 함수를 사용해서 결정 트리를 시각화할 수 있다.
▶ 결정 트리 해석

- 위와 같은 결정 트리 모델 결과가 있다고 가정하고 설명을 해보도록 하겠다.
- 루트 노드(Root Node): 깊이가 0인 맨 꼭대기의 노드
- 리프 노드(Leaf Node): 자식 노드를 가지지 않는 노드
- samples 속성: 얼마나 많은 훈련 샘풀이 적용되었는지
- value 속성: 노드에서 각 클래스에 얼마나 많은 훈련 샘플이 있는지
- Gini 속성: 불순도를 측정
- 즉, 한 노드의 모든 샘플이 같은 클래스에 속해 있다면, 이 노드를 순수(gini = 0)하다고 한다.
- ex) 위 그림에서, 깊이 2의 왼쪽 노드의 gini 점수는 1 - (0 / 54)^2 - (49 / 54) ^2 - (5 / 54) ^2 = 0.168

- 결정 트리의 장점은 데이터 전처리가 거의 필요하지 않다는 점이다.
- 특성의 스케일을 맞추거나 평균을 원점에 맞추는 작업이 필요하지 않다. (즉, feature scaling 불필요)
- 사이킷런은 이진 트리만 만드는 CART 알고리즘을 사용한다.
- 따라서 리프 노드(Leaf Node) 외의 모든 노드는 자식 노드를 2개씩 가진다.
- <참고> ID3와 같은 알고리즘은 둘 이상의 자식 노드를 가진 결정 트리를 만들 수 있다.
<참고>
- 모델 해석: 화이트 박스와 블랙 박스
- 화이트 박스 모델: 직관적이고 결정 방식을 이해하기 쉽다.
- ex) 결정 트리
- 블랙 박스 모델: 성능이 뛰어나고 예측을 만드는 연산 과정을 쉽게 확인할 수 있으나, 왜 그러한 예측을 만드는지를 설명하기 어렵다.
- ex) 랜덤 포레스트, 신경망
- 화이트 박스 모델: 직관적이고 결정 방식을 이해하기 쉽다.
▶ 클래스 확률 추정
- 결정 트리는 한 샘플이 특정 클래스 k에 속할 확률을 추정할 수도 있다.

- 예를 들어, 길이가 5cm이고 너비가 1.5cm인 꽃잎을 발견했다고 가정해보자.
- 이에 해당하는 리프 노드(Leaf Node)는 깊이 2에서 왼쪽 노드이다. (즉, 노란색 네모 박스 부분)
- 이 때, 각 클래스에 해당하는 확률을 계산해보면 다음과 같다.
- Iris-Setosa: 0% (= 0 / 54)
- Iris-Versicolor: 90.7% (= 49 / 54)
- Iris-Virginica: 9.3% (= 5 / 54)

▶ CART 훈련 알고리즘
- 사이킷런은 결정 트리를 훈련시키기 위해 CART(Classification and Regression Tree) 알고리즘을 사용한다.
- 먼저 훈련 세트를 하나의 특성 k의 임곗값 t_k를 사용해 두 개의 subset으로 나눈다.
- 그 다음, (크기에 따른 가중치가 적용된) 가장 순수한(gini = 0에 가까운) subset으로 나눌 수 있는 (k, t_k) 짝을 찾는다.
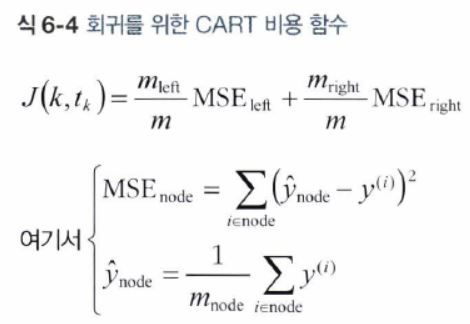
- 따라서 CART 알고리즘이 최소화해야 하는 비용 함수는 다음과 같다.
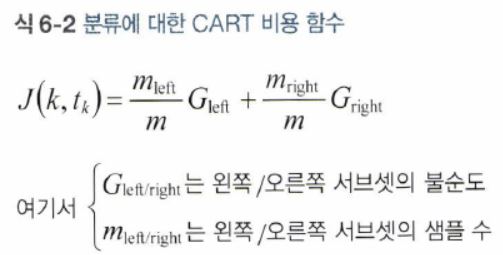
- CART 알고리즘이 subset을 나누는 과정은 (max_depth 매개변수로 정의된) 최대 깊이가 되면 중지하거나, 불순도를 줄이는 분할을 찾을 수 없을 때 멈추게 된다.
- max_depth 외에도 min_samples_split, min_samples_leaf, min_weight_fraction_leaf, max_leaf_nodes와 같은 매개변수도 중지 조건에 관여한다.
- CART 알고리즘은 탐욕적 알고리즘(greedy algorithm)이다.
- 탐욕적 알고리즘은 항상 최적의 솔루션을 보장하지 않는다.
- 또한 최적의 트리를 찾는 것은 NP-완전(NP-Complete) 문제로도 알려져 있다.
- 그러므로 "납득할 만한 좋은 솔루션"으로만 만족을 해야 한다.
▶ 계산 복잡도
- 결정 트리를 탐색하기 위해서는 약 O(log_2(m))개의 노드를 거쳐야 한다.
- 각 노드는 하나의 특성 값만 확인하기 때문에, 예측에 필요한 전체 복잡도는 특성 수와 무관하게 O(log_2(m))이다.
- 따라서 큰 훈련 세트를 다룰 때도 예측 속도가 매우 빠르다.
- 각 노드에서 모든 샘플의 모든 특성을 비교하면, 훈련 복잡도는 O(n x m x log(m))이 된다.
- 훈련 세트가 (수천 개 이하의 샘플 정도로) 작을 경우, 사이킷런은 (presort = True로 지정하면) 미리 데이터를 정렬하여 훈련 속도를 높일 수 있다.
- 하지만 훈련 세트가 클 경우에는 속도가 많이 느려진다.
▶ 지니 불순도 또는 엔트로피?
- 기본적으로 지니 불순도가 사용되지만, 엔트로피 불순도를 사용할 수도 있다.
- criterion 매개변수를 "entropy"로 지정하면 된다.
- 어떤 세트가 한 클래스의 샘플만 담고 있다면 엔트로피가 0이다.
- 가령, 아래 그림에서 깊이 2의 왼쪽 노드의 엔트로피는 - (49 / 54) * (log_2(49 / 54)) - (5 / 54) * (log_2(5 / 54) = 0.445이다.

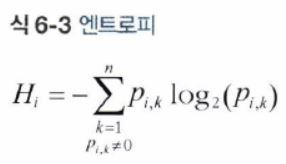
- 감소되는 엔트로피의 양을 정보 이득(information gain)이라고도 부른다.
<참고>
- DecisionTreeClassifier의 criterion 매개변수 default 값은 "gini"이고, DecisionTreeRegressor의 criterion 매개변수 default 값은 "mse"이다.
- 지니 불순도 vs 엔트로피 불순도
- 실제로는 큰 차이가 없다. 다만 지니 불순도가 좀 더 계산이 빠르므로 기본 값으로 사용하기 좋다.
- 그러나 다른 트리가 만들어지는 경우, 지니 불순도가 가장 빈도 높은 클래스를 한 쪽 가지(branch)로 고립시키는 경향이 있는 반면, 엔트로피는 조금 더 균형 잡힌 트리를 만든다.
▶ 규제 매개변수
- 결정 트리는 훈련 데이터에 대한 제약 사항이 거의 없다. (즉, 과대적합되기 쉽다)
- 결정 트리는 훈련되기 전에 파라미터 수가 결정되지 않기 때문에 Nonparametric Model이라고 한다.
- 훈련 데이터에 대한 과대적합을 피하기 위해, 모델 학습 시에 결정 트리의 자유도를 제한할 필요가 있다. (규제)
- 규제를 위해 조절할 수 있는 매개변수들은 다음과 같다.
- min_으로 시작하는 매개변수를 증가시키거나, max_로 시작하는 매개변수를 감소시키면 모델에 대한 규제가 커진다.
- max_depth: 결정 트리의 최대 깊이
- max_depth를 감소시키면 모델에 대한 규제가 커진다. (즉, 과대적합 위험 감소)
- min_samples_split: 분할되기 위해 노드가 가져야 하는 최소 샘플 개수
- min_samples_split을 증가시키면 모델에 대한 규제가 커진다. (즉, 과대적합 위험 감소)
- min_samples_leaf: 리프 노드가 가지고 있어야 할 최소 샘플 개수
- min_samples_leaf를 증가시키면 모델에 대한 규제가 커진다. (즉, 과대적합 위험 감소)
- min_weight_fraction_leaf: min_samples_leaf와 같지만, 가중치가 부여된 전체 샘플 수에서의 비율
- min_weight_fraction_leaf를 증가시키면 모델에 대한 규제가 커진다. (즉, 과대적합 위험 감소)
- max_leaf_nodes: 리프 노드의 최대 개수
- max_leaf_nodes를 감소시키면 모델에 대한 규제가 커진다. (즉, 과대적합 위험 감소)
- max_features: 각 노드에서 분할에 사용할 특성의 최대 개수
- max_features를 감소시키면 모델에 대한 규제가 커진다. (즉, 과대적합 위험 감소)
<참고>
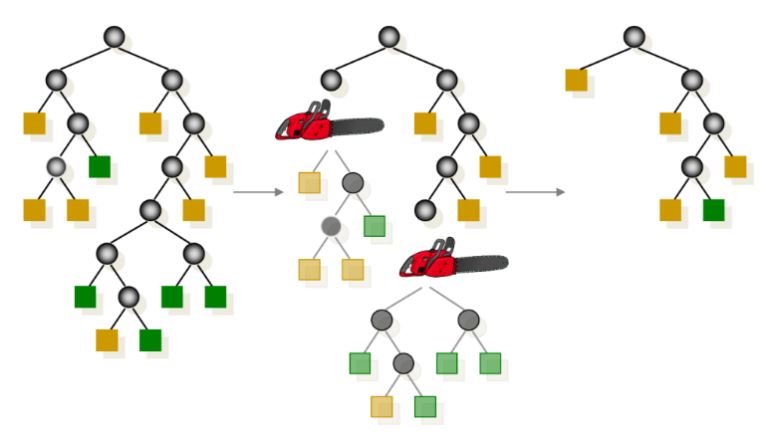
- 가지치기(Pruning)
- 트리가 너무 크면 훈련 세트에 과대적합할 위험이 있다.
- 따라서 순도를 높이는 것이 통계적으로 큰 효과가 없다면, 리프 노드 바로 위의 불필요한 노드는 제거(가지치기)해주어야 한다.
- 순도를 높이는 것이 유의미한지는 카이제곱 검정과 같은 통계적 검정을 사용하여 추정할 수 있다. (CHAID 알고리즘)
- 범주형 target 변수와 범주형 X 변수 간에 독립성 검정 시, 두 변수의 관계가 독립(즉, 귀무가설 기각 x)이라면 해당 X 변수는 target 변수에 중요한 영향을 미치지 않는 변수(즉, 모델링 과정에서 불필요한 변수)라고 판단할 수 있다.
- 카이제곱 검정은 sklearn.feature_selection.chi2 함수에 구현되어 있으니 참고하자.
- 이 때 p-value를 기준으로 p-value가 유의수준 alpha(일반적으로 0.05를 많이 사용)보다 높으면(귀무가설을 기각하지 못함), 해당 노드는 불필요한 것으로 간주되고 그 자식 노드는 삭제된다.
- 범주형 target 변수와 범주형 X 변수 간에 독립성 검정 시, 두 변수의 관계가 독립(즉, 귀무가설 기각 x)이라면 해당 X 변수는 target 변수에 중요한 영향을 미치지 않는 변수(즉, 모델링 과정에서 불필요한 변수)라고 판단할 수 있다.
- 순도를 높이는 것이 유의미한지는 카이제곱 검정과 같은 통계적 검정을 사용하여 추정할 수 있다. (CHAID 알고리즘)
- 가지치기(Pruning)은 불필요한 노드가 모두 없어질 때까지 계속된다.

EDA 시 Feature 선정 방법 (Python 기준) - Re-considered
1. Near Zero Variance (변수값의 분산을 보고 판단) 1000개 데이터중 990개에서 A의 값이 0, 10개에서 변수 A의 값이 1인 경우는 모델링에서 유용하지 않기 때문에 제거 columns = for column in columns: print('{} :
bongholee.com
<참고>
- 카이제곱 검정에 대하여...
- Goodness of Fit Test (적합도 검정)
- Test of Homogeneity (동질성 검정)
- Test of Independence (독립성 검정)
https://bioinformaticsandme.tistory.com/139
카이제곱검정 (Chi square test)
카이제곱검정 (Chi square test) Start BioinformaticsAndMe 카이제곱검정 (Chi square test) : χ² 검정은 카이제곱 분포에 기초한 통계적 방법 : 관찰된 빈도가 기대되는 빈도와 유의하게 다른지를 검증 :..
bioinformaticsandme.tistory.com
▶ 회귀 문제에서의 결정 트리
- 사이킷런의 DecisionTreeRegressor를 사용한다.
- 분류 트리와의 주요한 차이점은 각 노드에서 클래스를 예측하는 대신 어떤 값을 예측한다는 점이다.
- 가령, 아래의 회귀 결정 트리에서 x1 = 0.6인 샘플의 클래스를 예측한다고 가정해보자.
- 루트 노드부터 시작해서 트리를 순회하면, 결국 value = 0.111인 리프 노드에 도달할 것이다.
- 이 리프 노드에 있는 110개의 훈련 샘플의 평균 target 값이 예측값이 된다.
- 그리고 이 예측값을 사용하여 110개 샘플에 대한 평균제곱오차(MSE)를 계산하면 0.015가 된다.
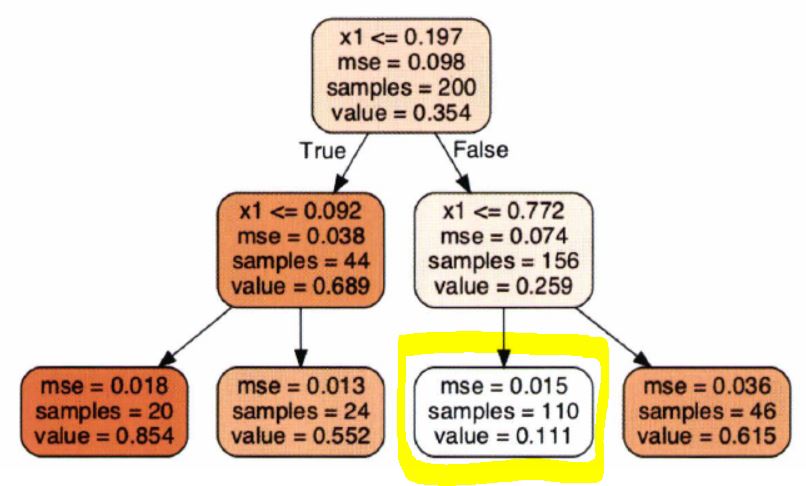
- 정리하면, 각 영역의 예측값은 항상 그 영역에 있는 target 값의 평균이 된다.
- 알고리즘은 예측값과 가능한 한 많은 샘플이 가까이 있도록 영역을 분할한다.
- 즉, 훈련 세트를 불순도를 최소화하는 방향으로 분할하는 대신, 평균제곱오차(MSE)를 최소화하도록 분할한다.
- CART 알고리즘이 최소화하기 위한 비용 함수는 다음과 같다.
- 회귀 문제에서도 결정 트리가 과대적합되기 쉽다.
- 이러한 과대적합 문제를 해결하기 위해서 모델에 대한 "규제"가 필요하다.
- 이해를 돕기 위해, 규제가 있는 경우와 없는 경우의 결정 트리 회귀 모델을 시각적으로 보여주도록 하겠다.

▶ 결정 트리 모델의 불안정성
- 결정 트리는 이해하고 해석하기 쉬우며, 사용하기 편하고, 성능도 뛰어나다.
- 하지만 결정 트리는 계단 모양의 결정 경계를 만들기 때문에, 훈련 세트의 회전에 민감하다.
- 아래의 그림과 같이 데이터 셋을 45도 회전시키면, 결정 트리 모델이 불필요하게 구불구불해지는 것을 확인할 수 있다.
- 이러한 경우의 결정 트리 모델은 잘 일반화될 수 없다.
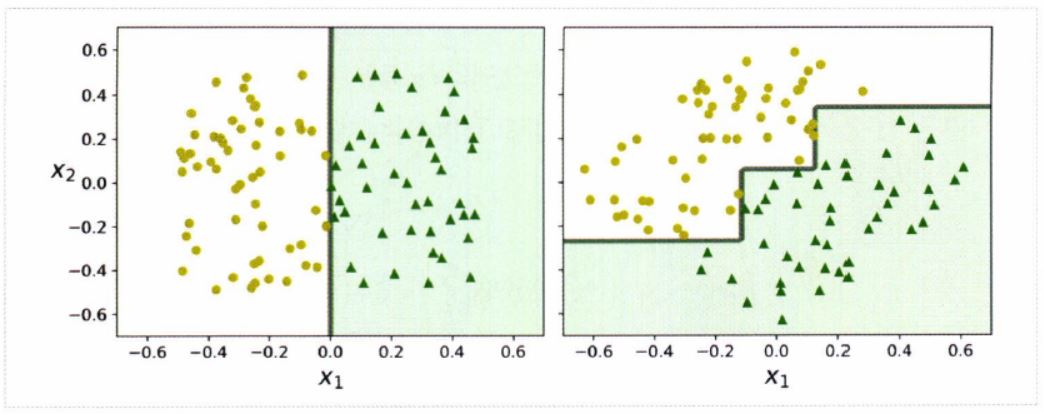
- 정리하면, 결정 트리 모델의 주된 문제점은 훈련 데이터에 있는 작은 변화에도 매우 민감하다는 것이다.
- 이런 문제를 해결하는 한 가지 방법은 훈련 데이터를 더 좋은 방향으로 회전시키는 PCA(주성분 분석) 기법을 사용하는 것이다.
- 또한 다음 장에서 배울 랜덤 포레스트는 많은 트리에서 만든 예측을 평균내서 이런 불안정성을 극복할 수 있다.
여기까지 해서 "6장. 결정 트리"에 대한 내용을 모두 정리해보았다.
다음 포스팅에서는 "7장. 앙상블 학습과 랜덤 포레스트"에 대해 정리해보도록 하겠다.
★ 참고 자료
- 핸즈온 머신러닝 2/E 교재
- 파이썬 머신러닝 완벽 가이드 교재
'Data Science > Machine Learning' 카테고리의 다른 글
| [핸즈온 머신러닝 2/E] 8장. 차원 축소 (0) | 2020.07.29 |
|---|---|
| [핸즈온 머신러닝 2/E] 7장. 앙상블 학습과 랜덤 포레스트 (0) | 2020.07.27 |
| [핸즈온 머신러닝 2/E] 5장. 서포트 벡터 머신 (0) | 2020.07.08 |
| [핸즈온 머신러닝 2/E] 4장. 모델 훈련 (0) | 2020.06.27 |
| [핸즈온 머신러닝 2/E] 3장. 분류 (0) | 2020.06.19 |



